WCSS is an abbreviation for Within Cluster Sum of Squares. It measures how similar the points within a cluster are using variance as the metric. It is the sum of squared distances of all dats points, within a cluster, with each other. in other words, WCSS is the sum of squared distances of each data point in all clusters to their respective centroids.
Month: January 2021
Discuss the different approaches for clustering
Following are the two approaches used by clustering algorithms:
- Agglomerative: The algorithms starts with assuming each individual point as a cluster and proceeds with adding the nearest point to the existing cluster. Thus similarity is used as a measure for creating new cluster. If not stopped, as per business requirement, the algorithm would go on to create one giant cluster with all the data points. This is also called bottoms up approach.
- Divisive: The algorithm starts with e one giant cluster with all the data points and proceeds to remove dissimilar points into separate clusters. Thus dissimilarity is used as a measure for creating new cluster. If not stopped, as per business requirement, the algorithm would go on to create individual cluster for all data points. This is also called top down approach.
What are the requirements to be met by a clustering algorithm?
Following are the set of requirements that a robust clustering algorithm should have:
- Scalability
- Ability to work with both categorical and continuous variables
- Ability to identify arbitrarily shaped clusters
- Should be robust to outliers and missing values
- Shouldn’t be affected by order of input data
- Ability to handle high dimensional data
- Easy to interpret
How does clustering play a role in supervised learning?
For large datasets with significant variance, it becomes difficult for one model to capture all the underlying patterns. In such cases it is advisable to break the dataset into homogenous subsets and then build separate model for each cluster. When we say homogenous, we mean homogeneity in terms of independent variables.
Thus we use clustering algorithms to split dataset into multiple homogenous subsets and build models customized to that subset.
What are the various applications of clustering?
Following are the use cases where clustering algorithms are applied
- Customer Segmentation
- Clustering datasets with high variance into clusters with relatively low variance and making separate model for each cluster. Thus getting better accuracy
- Anomaly detection/outlier detection
- Image Segmentation
- Data Analysis: It is easier to analyze homogenous data, identify trends and draw insights than doing it on heterogenous data with significant variance.
- Dimensionality Reduction: A variable having high affinity with a cluster would have low variance in that cluster. It can then be dropped without loss of information, if we’re building different models for each cluster. Or variables having similar cluster affinities can be grouped into single variable having aggregated cluster affinity as values, if we want to build a single model for the whole datset.
- For semi-supervised learning: You can use the same target variable for the whole cluster that a labelled observation belonging to that cluster has.
- Image Search Engines
What is clustering?
Clustering, in the context of machine learning, is the act of creating homogenous groups, with similar observations, from the heterogenous raw data. In clustering problems, the algorithm has to figure out the number of groups as well as what they are i.e. the factors that make the observations in the group similar to each other and distinct from other groups. The number of groups in clustering problems may change with the choice of algorithm.
What is an unsupervised learning approach? Why is it needed?
Unsupervised learning is a class of machine learning problems where there is no target variable. The algorithm has to figure out on its own whether its the patterns it needs to detect i.e. there is no variable to supervise the learning process towards a particular set of patterns.
In many real world scenarios we need unsupervised learning for ex we want to group stores similar stores, irrespective of their performance in terms of sales, on the basis of store attributes (size, number of cash counters, parking space etc.), macro economic and demographic factors. Here there is no target variable that you’re trying to predict or that is dependent on other variables, but a set of independent variables. In such cases unsupervised learning is needed.
Explain the step by step implementation of XGBoost Algorithm.
XGBoost is an abbreviation of Extreme Gradient Boosted trees. Now you may ask, what is so extreme about them? and the answer is the level op optimization. This algorithm trains in a similar manner as GBT trains, except that it introduces a new method for constructing trees.
Trees in other ensemble algorithm are created in the conventional manner i.e. either using Gini Impurity or Entropy. But XGBoost introduces a new metric called similarity score for node selection and splitting.
Following are the steps involved in creating a Decision Tree using similarity score:
- Create a single leaf tree.
- For the first tree, compute the average of target variable as prediction and calculate the residuals using the desired loss function. For subsequent trees the residuals come from prediction made by previous tree.
- Calculate the similarity score using the following formula:
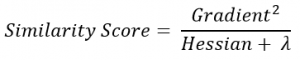where, Hessian is equal to number of residuals; Gradient2 = squared sum of residuals; λ is a regularization hyperparameter. - Using similarity score we select the appropriate node. Higher the similarity score more the homogeneity.
- Using similarity score we calculate Information gain. Information gain gives the difference between old similarity and new similarity and thus tells how much homogeneity is achieved by splitting the node at a given point. It is calculated using the following formula:
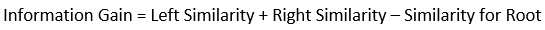
- Create the tree of desired length using the above method. Pruning and regularization would be done by playing with the regularization hyperparameter.
- Predict the residual values using the Decision Tree you constructed.
- The new set of residuals is calculated using the following formula:
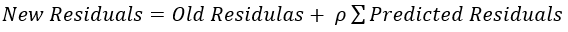where ρ is the learning rate. - Go back to step 1 and repeat the process for all the trees.
Why is XGBoost so popular?
Following are the advantages of XGBoost that contribute to its popularity:
- Exception to Bias Variance Trade off rule i.e. bias and variance can be reduced at the same time
- Computationally cost effective as it allows multi threading and parallel processing
- Allows hardware optimizations
- Allows early stopping
- Built in regularization factor
- Unaffected by multicollinearity. This becomes even more relevant given the vulnerability of Decision Trees to multicollinearity.
- Robust to outliers
- Robust to missing values
- Adept to sparse dataset. Feature engineering steps like one-hot encoding and others make data sparse. XGBoost uses a sparsity aware split finding algorithm to that manages sparsity patterns in the data
- Handles noise adeptly in case of classification problem
- Works both for regression and classification problems
- Works with both categorical and continuous variables.
- Package is just 7 years old and new features are added everyday.
Explain the step by step implementation of Gradient Boosted Trees.
Gradient Boosted Trees predict the residuals instead of actual values. Thus the algorithm calculates the gradient of the given loss function and tries to find the minima i.e. where the value of loss function is minimum, hence highest accuracy. It can work with a variety of loss functions. AdaBoost is a special case of GBT that works with exponential loss function.
Following are the steps involved in training of GBT for a regression problem:
- The algorithm starts with assuming the average of target column as prediction for all the observations. For subsequent trees the prediction value from step 6 is taken.
- Fit the tree, say G(x), on the resulting dataset
- Find the difference between actual values and the aforementioned average.
- Calculate the average of each leaf node [voting in case of classification problem]. The resulting values form the first set of pseudo residuals
- Take the pseudo residuals at the leaf nodes and calculate the hypothetical correct predictions for each leave node by subtracting the pseudo residual at that node from the older predicted value (prediction values from step 1)
- Calculate the new set of predictions(for target value) using the following formula:
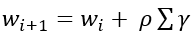
- Return to step 1 and repeat the process for all the M trees.
For the sake of simplicity, here we’ve taken simple subtraction as loss function, but any other loss function would work just as well.